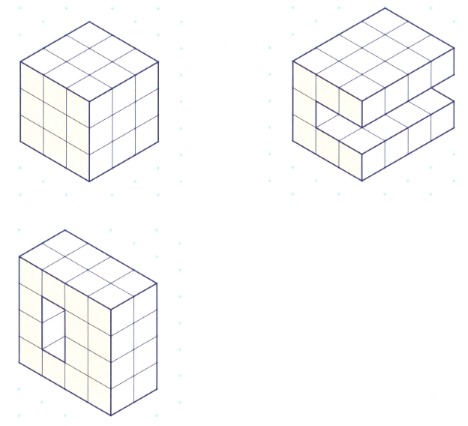
Representing 3D Shapes

The angle formed between the Isometric axes is?

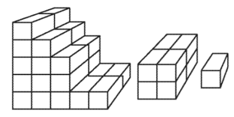
What is the smallest number of cubes that could be added to the diagram to make it into a cuboid.

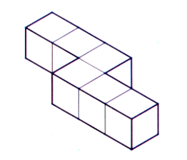
What is the smallest number of cubes that could be added to the diagram to make it into a cuboid.

In an isometric sheet dots form the pattern of:

Isometric sketch shows objects of:

How many cubes are there in the given figure?

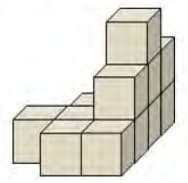
How many blocks are unseen in the given figure?

A cube painted red on two adjacent faces and black on the faces opposite to the red faces and green on the remaining faces is cut into sixty four smaller cubes of equal size. How many cubes have one face green and one of the adjacent faces black or red?

The dimensions of a cuboid are $5 \mathrm{cm}, 3 \mathrm{cm}$ and $2 \mathrm{cm}$. Draw the isometric sketches of this cuboid with $3 \mathrm{cm}\times 2 \mathrm{cm}\times 5 \mathrm{cm}$ configuration. 

The dimensions of a cuboid are $5 \mathrm{cm}, 3 \mathrm{cm}$ and $2 \mathrm{cm}$. Draw the isometric sketches of this cuboid with $5 \mathrm{cm}\times 3 \mathrm{cm}\times 2 \mathrm{cm}$ configuration. 

The dimensions of a cuboid are $5 \mathrm{cm}, 3 \mathrm{cm}$ and $2 \mathrm{cm}$. Draw the isometric sketches of this cuboid with $5 \mathrm{cm}\times 2 \mathrm{cm}\times 3 \mathrm{cm}$ configuration. 

The dimensions of a cuboid are $5 \mathrm{cm}, 3 \mathrm{cm}$ and $2 \mathrm{cm}$. Draw the isometric sketches of this cuboid with $3 \mathrm{cm}\times 5 \mathrm{cm}\times 2 \mathrm{cm}$ configuration. 

The dimensions of a cuboid are $5 \mathrm{cm}, 3 \mathrm{cm}$ and $2 \mathrm{cm}$. Draw the isometric sketches of this cuboid with $2 \mathrm{cm}\times 3 \mathrm{cm}\times 5 \mathrm{cm}$ configuration. 

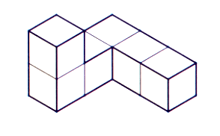
The diagram is made of six cubes. What is the smallest number of cubes that could be added to the diagram to make it into a cuboid.

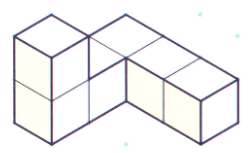
Lets say you have three identical cubes which you then join together so that each cube is covering atleast one face of another cube. How many faces of the three cubes are visible now?

How many axes are represented in isometric drawings?

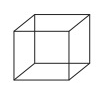
The isometric sketch of the above image is 

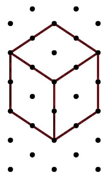
To count the number of cubes in each prism why is it important to know that all the diagrams show prisms?